

This can be used to calculate the area of a triangle when two sides and their included angle are known, as well as for other triangular equations. The altitude rule states that the product of the length of an altitude and its base is equal to the area of a triangle. By understanding the properties of a triangle and how they apply to various equations, students can gain a deeper understanding of geometry as a whole. Additionally, students may learn about different special types of triangles such as right triangles, isosceles triangles, and equilateral triangles. Each of these properties can be used to calculate other missing measurements within the triangle. Its properties include side lengths, angles, area, perimeter, and altitude. In Class 7, a triangle is defined as a three-sided polygon that has three angles and three sides. These lines divide the triangle into smaller triangles (called legs) and intersect at an orthocenter which is used for further calculations within triangular equations. The three altitudes of a triangle are lines that run from each vertex of the triangle down to the opposite side, or base line. What is triangle and its properties?Ī triangle is a three-sided polygon that has three angles and three sides. The intersection of these two legs forms what is known as an orthocenter. This line segment divides the triangle into two smaller triangles called legs. Its length is the same as the distance between that vertex and the base line. What is a altitude in geometry example?Īn example of a altitude in geometry is a line segment that runs from a vertex of the triangle down to the opposite side, or base line. The five properties of a triangle are side lengths, angles, area, perimeter, and altitude. Then measure this line with a ruler or tape measure this will give you the altitude of your triangle.
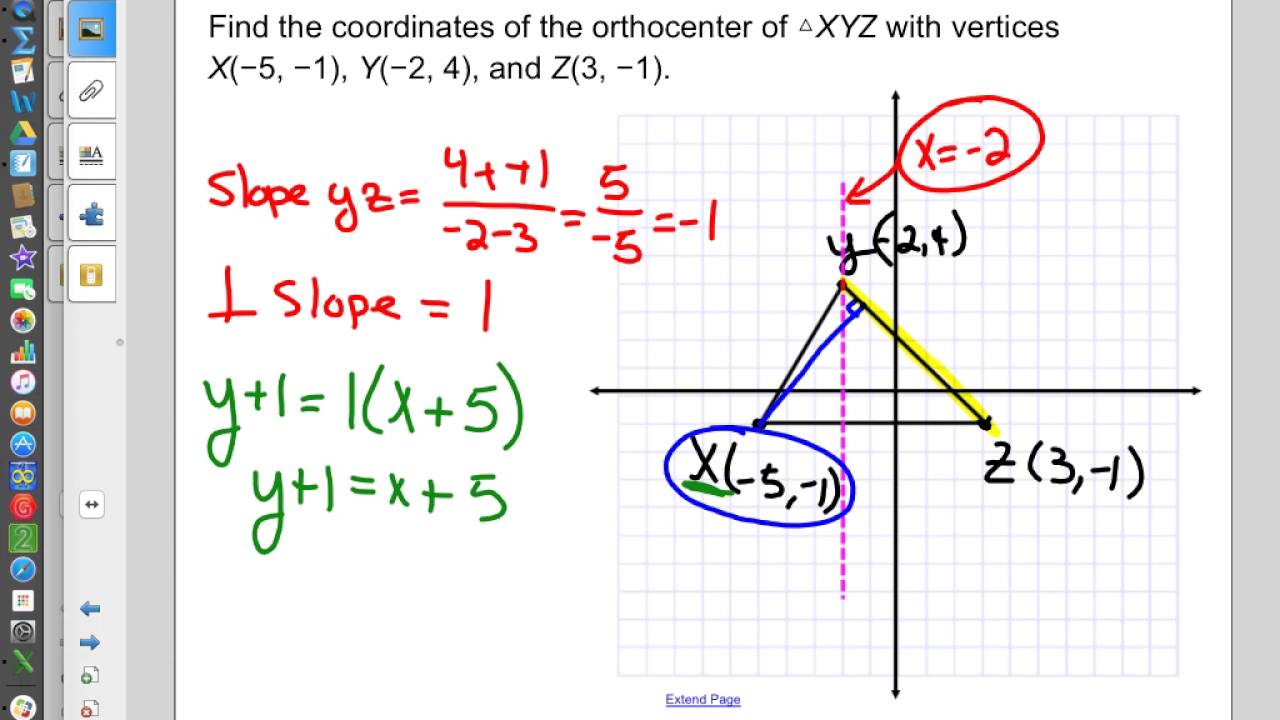
To find the altitude of a triangle in geometry, start by choosing one of its vertices and draw a line from that vertex down to the opposite side.
#Defnition of altitude geometry how to
Knowing how to calculate altitude and how it applies to various equations will make it easier for students to understand more complex geometrical problems and principles later on down the road! With a little practice and some knowledge about how altitudes work, students will be well on their way towards mastering geometry concepts involving triangles! FAQ How do you find the altitude of a triangle in geometry? It also helps form an orthocenter which can be used for further calculations within triangle equations and problems.
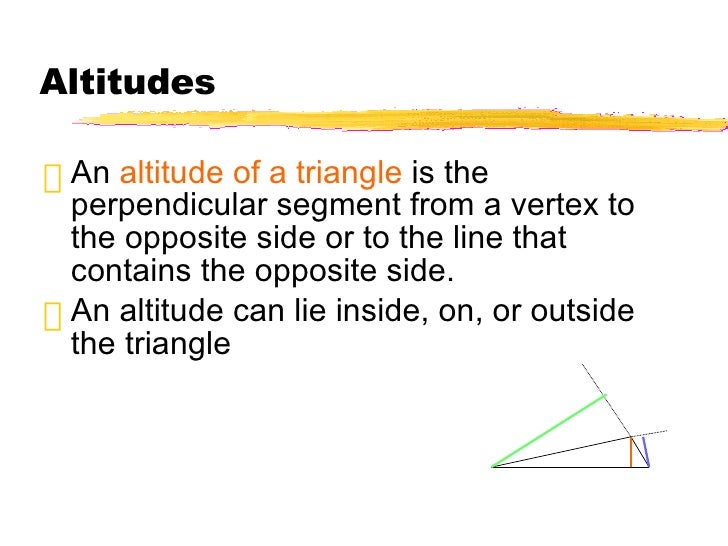
Conclusion:Īltitude is an important concept in geometry because it can be used to calculate missing measurements within triangles. Once you have the altitude measurement, you can use this information to find out other missing measurements in your triangle such as angle measurements or side lengths. To calculate the altitude of a triangle, start by choosing one of its vertices and draw a line from that vertex down to the opposite side. The altitude also serves another purpose its length can be used to calculate any missing side lengths in right triangles. The intersection of these two legs forms what is known as an orthocenter, which is used when measuring angles in triangles. What is Altitude?Īltitude is a line segment that runs from a vertex of the triangle down to the opposite side, or base line.
Read on for a quick introduction to altitude in triangles. Altitude is an important concept in geometry, and understanding it can help you understand many other geometric concepts as well. Have you ever heard the term “altitude” in a geometry lesson? If so, you may be wondering what it means and how it applies to triangles.


 0 kommentar(er)
0 kommentar(er)
